欧拉方程

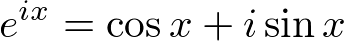
欧拉方程是数学中最引人注目和最神秘的发现之一。欧拉方程（公式）显示了三角函数和复指数函数之间的深层关系。

欧拉方程的发现

首先，看一下指数函数的e^x以及三角函数 sin(x） 和 cos(x）的泰勒级数表示。

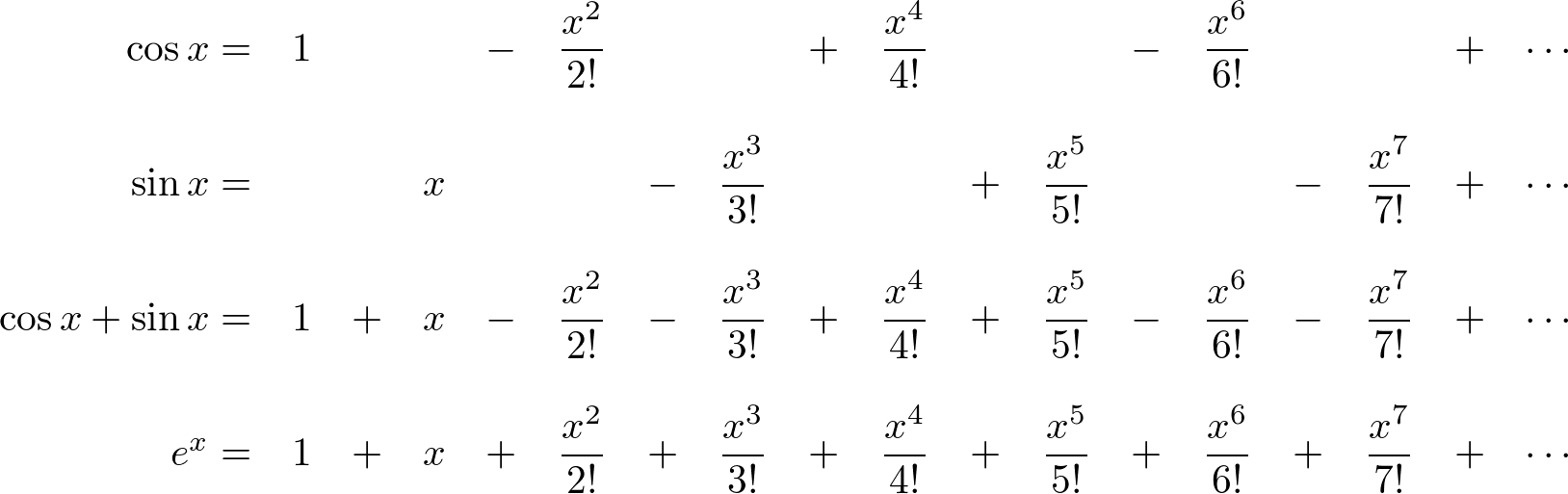
e^x与 cos(x)+sin(x) 进行相比较，项目和参数无全相同，但符号除外。
数学家试图弄清楚指数函数和 2 个振荡函数之和之间的这种奇怪关系。最后，欧拉Euler 通过将虚数虚数i引入上述泰勒级数来完成这一关系;

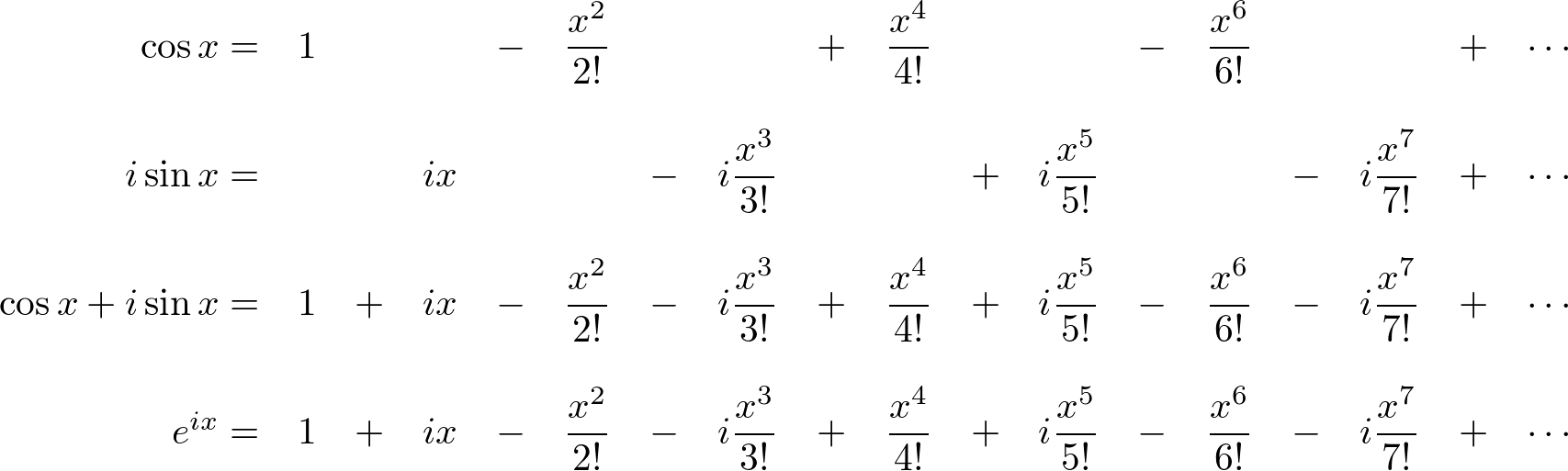
所以，就得以了欧拉方程。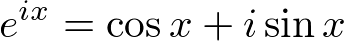

欧拉方程图

我们知道指数函数e^x随着 x 的增长呈指数级增长。但是，这个函数e^{ix}是什么样的呢？

下图显示了复指数函数 复指数函数，e^{ix}的图形，方法是在 3D 复空间（x - 实数 - 虚轴）中绘制 的e^{ix}泰勒级数。令人惊讶的是，它是一个螺旋弹簧（线圈）形状，围绕一个单位圆旋转。并且，当它被投影到实数（顶视图）和虚数轴（侧视图）时，它变成了一个三角函数，分别是余弦和正弦。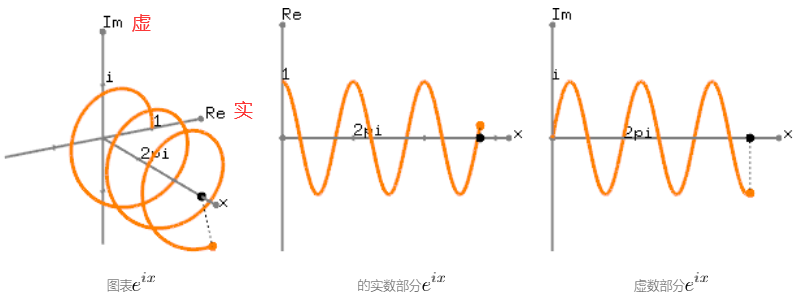

复指数函数的图形表示清楚地表示e^{ix}复指数函数，e^{ix}显示了与三角函数的关系;e^{ix}实数部分是余弦，虚部是正弦函数，周期2pi为弧度。

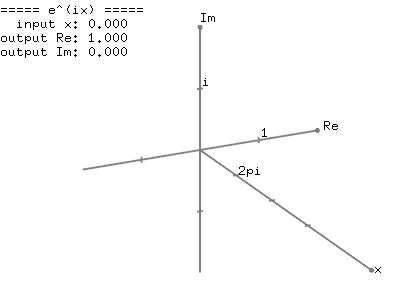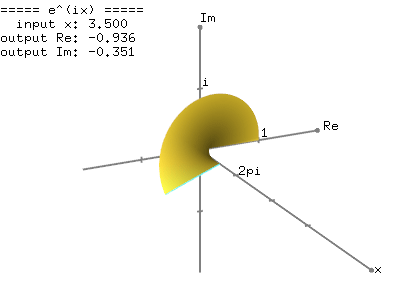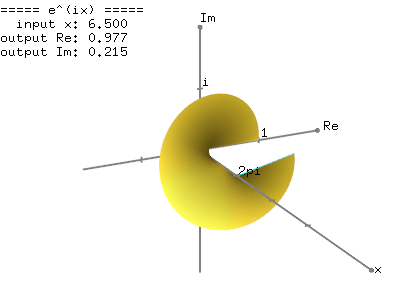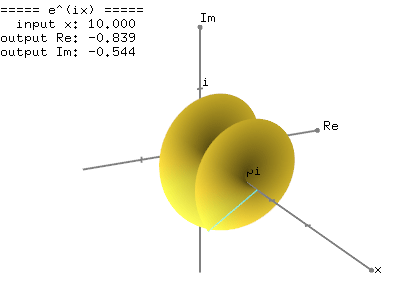
您可以下载源代码和二进制文件：https://www.vaczh.com/uploadimg/202502/euler.zip

欧拉方程的含义

当e^{ix}投影到复平面时，是一个单位圆，并且周期为2Pi，这意味着当指数x增加delt变化时，会产生delt的弧度变化。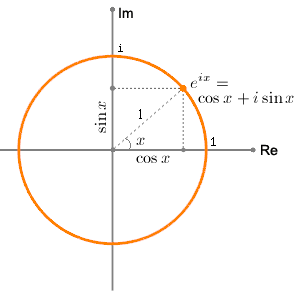

这种非常方便地表示了表示旋转物体或周期信号。并且在数学运行上，将乘法简化为加法运行。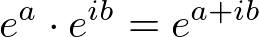

复指数形式经常用于电气工程和物理学。例如，在傅里叶分析中，周期信号可以表示为正弦和余弦函数之和，并且附加到弦的质数的运动也是正弦的。这些正弦函数可以用复杂的指数形式代替，以简化计算。

我们可以将这种模型表示扩展到任何复数。

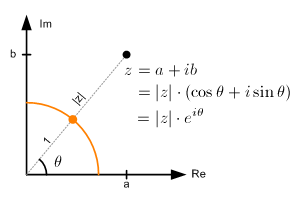
大小（范数|z|的复数是一个标量值，可以使用指数和对数定律来表示：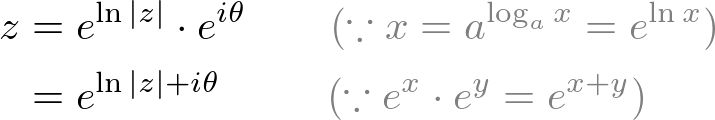

使用欧拉方程的 2D 旋转

由上面可知，对于任意复数a+bi都可以用e^{ix}表示，这时两个复数的相乘就表示如下：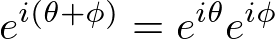

所以乘法变成了加法，变成了角度的旋转。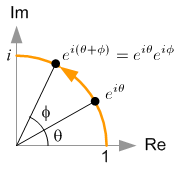

那么对于任意复数z=x+iy，读转一定角度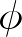我们只需乘以该数字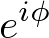即可，
然后，旋转后的结果 z’ 变为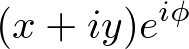

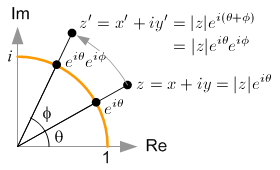
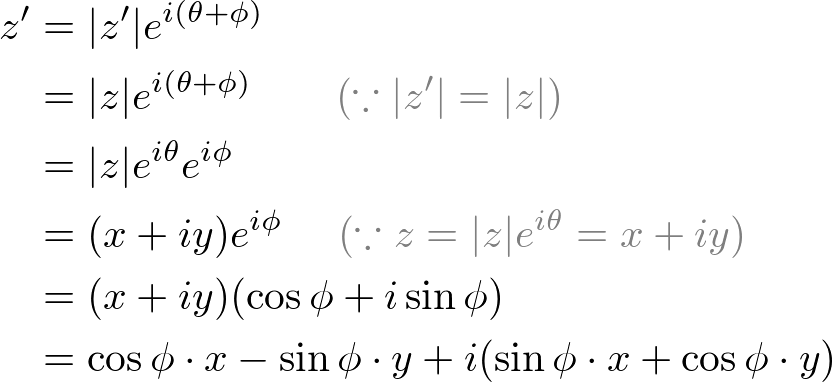
如果我们通过省略，将其重写为矩阵形式虚数 i，它就会变成我们熟悉的 2x2 旋转矩阵。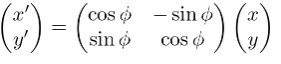

欧拉方法的特例

如果我们将该值x=pi代入 Euler 方程，则得到：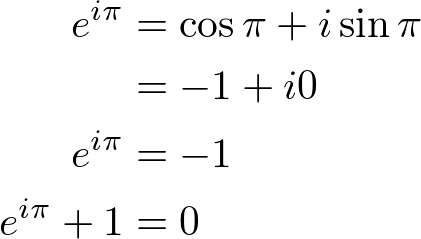

这个方程称为 Euler Identity ，显示了 5 个基本数学常数之间的联系;0、1、 圆周率、 e和 我.

对数函数仅针对域 x > 0 定义。但是，Euler Identity 允许通过将指数转换为对数形式来定义负 x 的对数：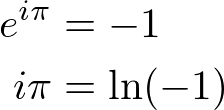

i当x=pi/2时

欧拉方程的证明

欧拉方程是通过微积分证明的。